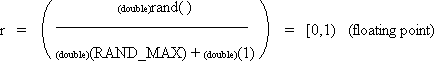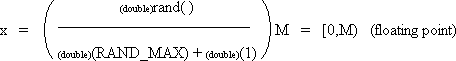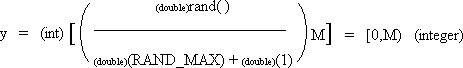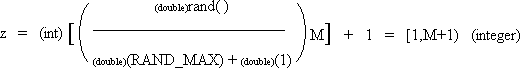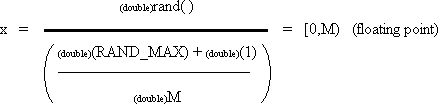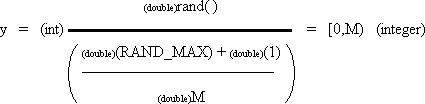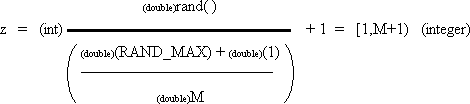USING THE C OR C++ rand() FUNCTION

GENERATING RANDOM INTEGERS WITHIN A DESIRED RANGE ADDITIVE CONGRUENTIAL RANDOM NUMBER GENERATORS
index
Back to Deley's Homepage



USING THE C OR C++ rand() FUNCTION

The ANSI C standard only states that rand() is a random number generator which generates integers in the range [0,RAND_MAX] inclusive, with RAND_MAX being a value defined in stdlib.h, and RAND_MAX being at least 32767. Note that 32767 isn't a very big number. If RAND_MAX is only 32767 then you can probably get only about 20,000 random numbers before the sequence starts to lose its randomness. Note that RAND_MAX may be larger. Check what the value of RAND_MAX is for you. A rule of thumb is you can generate around 2/3 of RAND_MAX random numbers before it becomes obvious what the remaining numbers are going to be and the sequence loses its randomness. To be safe I recommend generating no more than 1/10 of RAND_MAX random numbers.1

If you need to generate more than 1/10 of RAND_MAX random numbers then have a look at the newer and better portable random number generators at SOURCE CODE AND DISCUSSION OF NEWER & BETTER RANDOM NUMBER GENERATORS

DETERMINING VALUE OF RAND_MAX
#include <stdio.h>
#include <stdlib.h>
main()
{
    printf("RAND_MAX = %u\n", RAND_MAX);
}


EXAMPLE USE OF THE C AND C++ rand() FUNCTION:
#include <stdio.h>
#include <stdlib.h>

main()
{
/* DEFINE VARIABLES */
   int seed;         /* Choose any integer value for seed to initialize the random number generator with. The same value of seed will always produce the same sequence of random numbers. To get a different sequence of random numbers next time, choose a different value of seed.

Note: on Microsoft Visual C++ 6.0, if seed is negative then a seed value from the system clock is used. Also check for a randomize() function on your compiler. */

double r;/* random value in range [0,1) */

long int M;/* user supplied upper boundary */

double x;/* random value in range [0,M) */
int y;/* random integer in range [0,M) if M is an integer then range = [0,M-1] */
int z;/* random integer in range [1,M+1) if M is an integer then range = [1,M] */
int count;/* just a variable we need to count how many random numbers we've made for this example */
/*BEGIN CODE*/
seed = 10000;/* choose a seed value */
srand(seed);/*initialize random number generator*/

M = 1000;/* Choose M. Upper bound. (M should be much less than RAND_MAX. See below.) */
   for(count=1; count<=20; ++count)
{
       r = (   (double)rand() / ((double)(RAND_MAX)+(double)(1)) );
                                   /* r is a random floating point value in the range [0,1) {including 0, not including 1}. Note we must convert rand() and/or RAND_MAX+1 to floating point values to avoid integer division. In addition, Sean Scanlon pointed out the possibility that RAND_MAX may be the largest positive integer the architecture can represent, so (RAND_MAX+1) may result in an overflow, or more likely the value will end up being the largest negative integer the architecture can represent, so to avoid this we convert RAND_MAX and 1 to doubles before adding. */
       x = (r * M);
                                   /* x is a random floating point value in the range [0,M) {including 0, not including M}. */
       y = (int) x;
                                   /* y is a random integer in the range [0,M) {including 0, not including M}. If M is an integer then the range is [0,M-1] {inclusive} */
       z = y + 1;
                                   /* z is a random integer in the range [1,M+1) {including 1, not including M+1}. If M is an integer then the range is [1,M] {inclusive} */
       printf("random number %3d %5f %5f %5d %5d\n",count,r,x,y,z);
   }
}

You can expand or contract the range by choosing a value for M. You can shift the range up or down the number line by adding or subtracting a fixed value. You can even flip the range over by multiplying by -1.

Note: Do NOT use

      y = rand()  %  M;

as this focuses on the lower bits of rand(). For linear congruential random number generators, which rand() often is, the lower bytes are much less random than the higher bytes. In fact the lowest bit cycles between 0 and 1. Thus rand() may cycle between even and odd (try it out). Note rand() does not have to be a linear congruential random number generator. It's perfectly permissible for it to be something better which does not have this problem.

We can combine the above equations to create formulas for r,x,y,z:

r = [0,1) = {r: 0 <= r < 1} real
x = [0,M) = {x: 0 <= x < M} real
y = [0,M) = {y: 0 <= y < M} integer
z = [1,M] = {z: 1 <= z <= M} integer




Note we need to force floating point division by casting rand() and/or RAND_MAX+1 as a (double). In addition, Sean Scanlon pointed out the possibility that RAND_MAX may be the largest positive integer the architecture can represent, so (RAND_MAX+1) may result in an overflow, or more likely the value will end up being the largest negative integer the architecture can represent, so to avoid this we convert RAND_MAX and 1 to doubles before adding.







For y if M is an integer then the result is between 0 and M-1 inclusive.
For z if M is an integer then the result is between 1 and M inclusive.

Note the order in which we do the calculations. We do not want to calculate [rand() * M] as the result may overflow the largest integer value our computer can represent. The formulas for x,y,z, can also be calculated as:







Here we calculate [(double)(RAND_MAX) + (double)1] / (double)M and then divide rand() by that result.
Again for y if M is an integer then the result is between 0 and M-1 inclusive.
Again for z if M is an integer then the result is between 1 and M inclusive.

Dave Beleznay pointed out that if M is larger than RAND_MAX, you'll have gaps in the results (there will be integers in the range that are never returned). Also, for very large values of M, you'll have the additional problem that RAND_MAX / M appoaches zero and an underflow error may occur (the result the computer gives you will actually be zero rather than a very very tiny number, setting you up for a divide by zero error).

Note once more: Do NOT use

      y = rand()  %  M;

as this focuses on the lower bits of rand(). For linear congruential random number generators, which rand() often is, the lower bytes are much less random than the higher bytes. In fact the lowest bit cycles between 0 and 1. Thus rand() may cycle between even and odd (try it out). Note rand() does not have to be a linear congruential random number generator. It's perfectly permissible for it to be something better which does not have this problem. [NOTE: Any implementation of the C programming language is not required to use the formula given in 4.1.3, it is merely a suggestion. Your implementation of the C language may use a completely different formula to generate pseudo-random numbers.]

footnotes:
1
[Note from Bret, 2008-09-14]: Technically, this isn't necessarily true. The standard only indicates that rand() is required to return at least 15 bits of useful data at a time. It does not mandate that the internal state of rand() is only 15 bits. Even if you generate RAND_MAX - 1 values, you cannot predict what the next value will be if rand() has an internal state that is more than 15 bits.

For example, an ANSI-compliant library could implement rand() using Mersenne Twister which has a period of 2^19937-1, but still only return [0, 32767] from rand() simply by masking off the lower 15 bits from each value that it generates.

The main problem with rand() is that it could be using only 15 bits of state and therefore could be repeating itself every 32768 values. The standard doesn't require anything better than that, and many implementations of it are of poor quality. That's why it has been superceded by random() which is more explicit about how it is implemented. So the rule-of-thumb I would recommend is "don't use it".

If you're stuck with it, one way to enhance the range but still avoid the "gaps" problem you mentioned would be to do something like this:

  double MAX = (double)RAND_MAX;
  double r = (((rand() / MAX + rand()) / MAX + rand()) / MAX + rand()) / MAX;

Calling rand() four times gives you at least 60 bits of info, which is enough to saturate the precision of double (53 bits in the mantissa). It's still not recommended, though.

If you want to avoid using slow floating-point calculations but still avoid the problem with using "%" to generate an integer sub-range, you could scale the integer range up to make it as close to RAND_MAX as possible, repeatedly call rand() until you get a value less than the scaled-up range, and then scale the result back down. If the range is greater than RAND_MAX you can do the same thing up to RAND_MAX * RAND_MAX with numbers generated with rand() * (RAND_MAX+1) + rand().

Pseudo-code:


int range = max - min;
if (range < RAND_MAX)
{
  int scale = (RAND_MAX + 1) / range;
  int scaledRange = scale * range;
  while (true)
  {
     int r = rand();
     if (r < scaledRange) return r / scale + min;
  }
}
 
int RAND_MAX_2 = (RAND_MAX + 1) * (RAND_MAX + 1) - 1;
 
if (range < RAND_MAX_2)
{
  int scale = (RAND_MAX_2 + 1) / range;
  int scaledRange = scale * range;
  while (true)
  {
     int r = rand() * (RAND_MAX + 1) + rand();
     if (r < scaledRange) return r / scale + min;
  }
}
 

That second half only works if RAND_MAX_2 fits within the size of int, which it usually won't if RAND_MAX > 65535.



GENERATING RANDOM INTEGERS WITHIN A DESIRED RANGE ADDITIVE CONGRUENTIAL RANDOM NUMBER GENERATORS
index
Back to Deley's Homepage
Revised September 2022